درس سی و یکم دروس هیئت
طول و عرض بلاد
این درس تتمّه درس پیش است. در توضیح گفتار بیرجندی گوییم:
قوله: هو قوس منها، یعنی عرض بلد در حقیقی قوسی از دائره نصف النهار است الخ.
قوله: من جانب لاأقرب منه، این تعبیر شامل آفاق رحوی است. اما اگر می گفت: من الجانب الأقرب شامل آفاق رحوی نمی گردید.
قوله: وهی مساویه لقوس منها الخ، یعنی قوس عرض بلد با قوسی از دائره نصف النّهار که واقع بین سمت قدم و دائره معدل از جانبی که اقرب از آن نیست می باشد، برابر است.
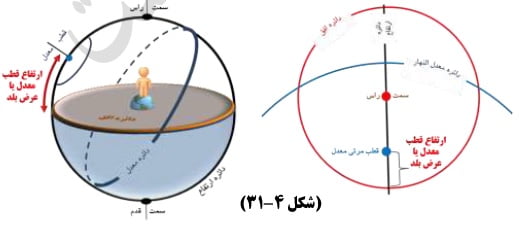
بنابراین که دائره نصف النهار به دو قطب افق تنصیف می گردد چنانکه با خود دائره معدل النهار نیز تنصیف می گردد پس بعد از اسقاط قوس مشترک از دائره نصف النهار بین نصفین، دو قوس باقی مساوی یکدیگر خواهند بود.الف
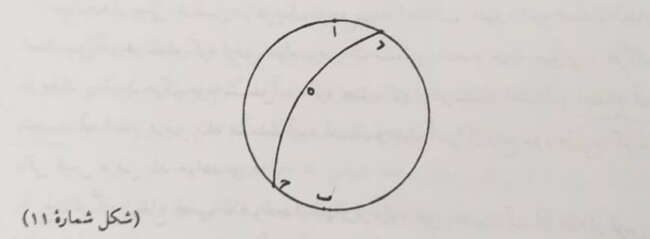
فرض بفرمایید در (ش ۱۱) -ا- سمت الرأس، و -ب- سمت القدم، و -ا د ب ج- دائره نصف النهار، و -د ه ج- معدل النهار، و -ا د ب- نصف دور است چنانکه -د ب ج-، و قوس -د ب- مشترک بین آن دو است، پس بعد از القاء آن -ا د- که عرض بلد است با -ب ج- مساوی می باشد.
قوله: و ایضا هی مساویه لارتفاع الخ قوسی از دائره نصف النهار که واقع بین دائره افق و سمت رأس است ربع دور است. و همچنین قوسی از دائره نصف النهار که واقع بین دائره معدل النهار و قطب ظاهر آنست ربع دور است پس این دو قوس با هم مساوی اند که هر یک ربع دور است. و قوسی از دائره نصف النهار که بین قطب ظاهر معدل النار و سمت رأس است مشترک بین دو قوس مذکور است.
پس چون این مقدار مشترک بین دو ربع را القاء کنیم دو قوس باقی یعنی ارتفاع قطب معدل مساوی با قوس بعد سمت رأس از دائره معدل از جانب اقرب یعنی عرض بلد خواهد بود. و بحث از انحطاط قطب معدل النهار از دائره افق و مساوی بودن آن با عرض بلد نیز بر این منوال است.ب
قوله: ولهذا اطلق علی واحد منها انها عرض البلد، یعنی بر هر یک از آن چهار قوس که یکی به حقیقت و سه دیگر بلحاظ مساوی بون آنها با قوس حقیقی عرض بلد به تفصیلی که در درس سی گفته آمد.
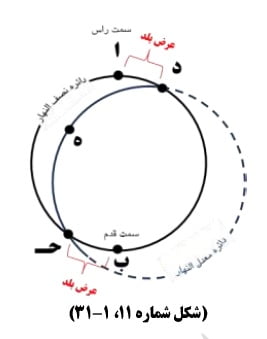
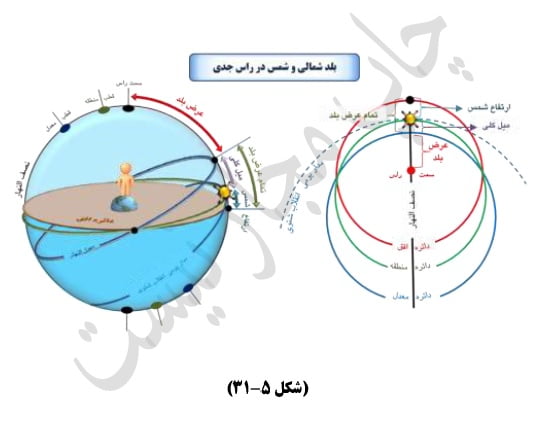
ب- مدار یومی شمس در هر یک از دو نقطه اعتدال، خود دائره معدل النهار است پس در هر نقطه کره ارض خواه عرض آن شمالی باشد و خواه جنوبی، هرگاه در وقت رسیدن مرکز جرم شمس به دائره نصف النهار در نقطه اعتدال، ارتفاع آن بدست آید تمام عرض بلد بدست آمده است، و چون آنرا از ربع دور طرح کنیم باقی قوس عرض بلد خواهد بود.ج
ج- هرگاه ارتفاع قطب ظاهر معدل النهار از دائره افق بدست آید آن مقدار قوس ارتفاع قطب مساوی عرض بلد خواهد بود مطلقاً اعنی خواه عرض بلد شمالی بوده باشد و خواه جنوبی، و خواه عرض بلد بمقدار میل کلی باشد و خواه کمتر از آن و خواه بیشتر از آن.د
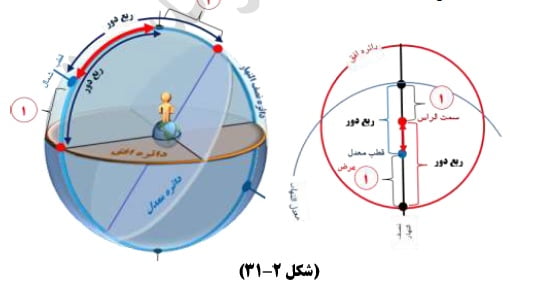
د- دانسته ایم که دائره ماره به اقطاب اربعه از دو نقطه انقلاب صیفی و انقلاب شتوی می گذرد، و اقصر قوسی از آن که در میان معدل النهار و منطقه البروج است قوس میل کلی است به تفصیلی که در درس ۸ و ۹ گفته آمد. پس قوس میان دو نقطه یاد شده از دائره ماره به اقطاب اربعه از جانب اقرب ضعف قوس میل کلی است که معدل النهار از منتصف آن می گذرد.
حال اگر شمس در رأس الجدی بود یعنی مدار یومی او مدار رأس الجدی بود و عرض بلد شمالی بوده باشد، و یا در رأس السرطان یعنی مدار یومی شمس مدار رأس السرطان بود و عرض بلد جنوبی باشد، هرگاه مرکز جرم شمس در یکی از آن دو نقطه یعنی در نقطه رأس الجدی و بلد شمالی باشد و یا بالعکس در نقطه رأس السرطان و بلد جنوبی، بر دائره نصف النهار بود -و دانسته ای که دائره نصف النهار با دائره ارتفاع در این هنگام متحد خواهند بود- پس اگر ارتفاع شمس را در آن هنگام تحصیل کنیم و میل کلی را بر آن بیفزاییم و مجموع را از نود طرح کنیم حاصل قوس عرض بلد مفروض خواهد بود مطلقاً.
یعنی برای آفاق شمالی مقدار عرض بلد شمالی، و برای آفاق جنوبی مقدار عرض بلد جنوبی، خواه مقدار عرض بلد کمتر از میل کلی باشد و خواه برابر آن و خواه زائد بر آن.
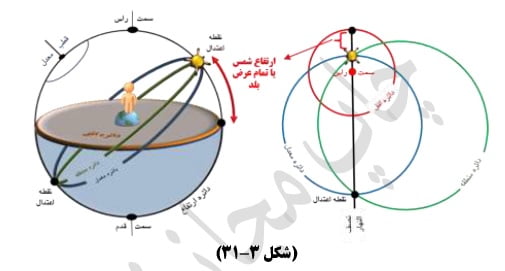
بیان: چون عرض بلد اقصر قوسی از دائره نصف النهار است که میان سمت الرأس یعنی قطب ظاهر افق، و میان معدل النهار افتد، لاجرم ارتفاع دائره معدل النهار از افق تمام عرض بلد خواهد بود و چون ارتفاع شمس را در هنگام موافات مرکز آن بدائره نصف النهار -در فرض مذکور- أخذ کرده ایم و میل کلی را بر آن افزوده ایم حاصل ارتفاع دائره معدل النهار می باشد که تمام عرض بلد است و چون آنرا از نود بکاهیم قوسی باقی، خود عرض بلد خواهد بود.ه
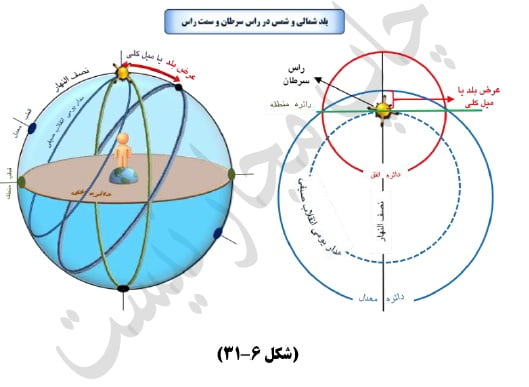
ه- اگر مدار یومی شمس رأس سرطان بود و بلد شمالی بود و نصف النهار آن روز به سمت رأس بلد رسد اشخاص را در آن هنگام سایه نبود پس معلوم شود که عرض بلد شمالی به مقدار میل کلی بود. و بالعکس هرگاه مدار یومی شمس رأس جدی بود و به موافات مرکز جرم شمس به دائره نصف النهار بر سمت رأس بلد مفروض بود و اشخاص را در آنهنگام سایه نبود پس معلوم شود که عرض بلد جنوبی به قدر میل کلّی بود.و
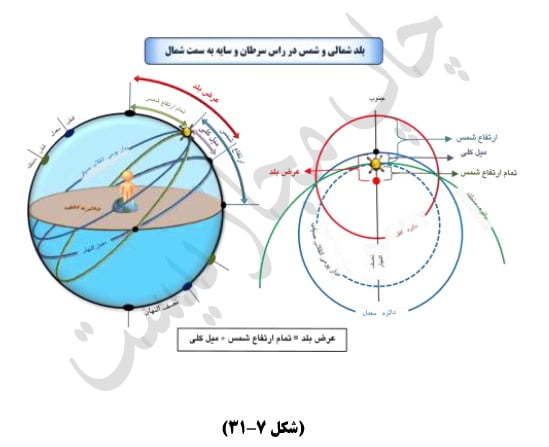
و- هرگاه مدار یومی شمس مدار رأس سرطان بود و بلد شمالی باشد و اشخاص را در هنگام موافات مرکز جرم شمس بدائره نصف النهار سایه بسوی قطب شمال افتد قرض شمس به جانب جنوب آنان بود، پس معلوم گردد که عرض بلد شمالی مفروض بیش از میل کلی است. لذا اگر ارتفاع شمس را در آنگاه بگیریم و تمام آن را تا سمت رأس تحصیل کنیم یعنی از ربع دور بکاهیم و بر حاصل میل کلی را بیافزائیم، این مجموع میل کلی و تمام ارتفاع شمس عرض بلد شمالی مفروض خواهد بود.ز
و به همین وزان و بیان اگر بلد جنوبی باشد و مدار یومی شمس مدار رأس جدی بود مقدار عرض بلد جنوبی مفروض بدست آید.
بیان (دروس هیئت و دیگر رشته های ریاضی – درس ۳۱ طول و عرض بلاد)
الف)
بیان:
ب)
بیان:
ج)
بیان:
د)
بیان:
ه)
بیان:
و)
بیان:
ز)
بیان:
یادداشت
لازم به ذکر است که مطالب قید شده فوق تحت عنوان بیان، نکات و … پیرامون درس ۳۱ طول و عرض بلاد از دروس هیئت و دیگر رشته های ریاضی در حد فهم این نگارنده حقیر است، بنابراین اکیداً توصیه میگردد علاوه بر مطالعه اصل کتاب، پیگیری مستمر جلسات تدریس استاد صمدی آملی در خصوص شرح کتاب دروس هیئت و دیگر رشتههای ریاضی جناب علامه حسنزاده آملی، به مباحثه نیز بپردازید.
کتاب دروس هیئت و دیگر رشتههای ریاضی علامه حسنزاده آملی که توسط استاد صمدی آملی تدریس شده است.
برای مطالعه درس سی و دوم دروس هیئت و دیگر رشته های ریاضی اینجا را کلیک کنید.
مجله اینترنتی تحلیلک








