پیرامون میل (عرض و بعد کوکب)
این مطلب به درس دوازدهم کتاب دروس هیئت و دیگر رشته های ریاضی علامه حسن زاده آملی با عنوان پیرامون میل (عرض و بعد کوکب) اختصاص دارد.
درس ۱۲
پیرامون میل
در درس پیش دانسته ایم که عرض کوکب فاصله او از فلک بروج یعنی منطقه البروج است، پس اگر کوکبی بر نفس دائره بروج بود وی را عرض نبود، چنانکه اگر کوکب بر نفس دائره معدل النهار بود وی را بعد نبود.
و چنان که در درس پنجم دانسته شد، خورشید همیشه در سطح دائره بروج است و هیچگاه مدار او از مدار فلک بروج اعنی منطقه البروج خارج نمی شود که بدین سبب دائره بروج را دائره شمسیه نامیده اند، نتیجه این که شمس را هیچگاه عرض نبود.
پس از دروس گذشته دانسته شده است که: اگر کوکب بر نفس معدل النهار بود آن را بعد نبود. و اگر بر نفس منطقه البروج بود آن را عرض نبود. و اگر بر یکی از دو نقطه اعتدال بود او را نه بعد بود و نه عرض. و اگر بر یکی از دو نقطه منقلب بود بعد او به قدر میل کلی بود. و اگر بر یکی از دو نقطه نظیره انقلاب بود عرض او به قدر میل کلی بود. و اگر بر قطب معدل بود بعد او ربع دور بود. و اگر بر قطب منطقه بود عرض او ربع دور بود. و نهایت بعد شمس از معدل النهار در دو نقطه منقلب صیفی و شتوی بود، و به عبارت دیگر: نهایت بعد شمس به قدر میل کلی خواهد بود. و چون به اعتدالین آید بر سطح معدل النهار بود بی بعد.الف
تبصره: گمان نرود که چون میل اول اجزای منطقه البروج از معدل النهار بدست آمد، دیگر چه نیاز به تحصیل میل ثانی، چه این که بعد مسافتی از مبدأی تا منتهای معلوم شده است بعد عکس آن همانست که بعد اصل بوده است؟
رفع گمان این که: این سؤال در دو نقطه منقلب و نظیره آنها صادق است زیرا که دوائر میل و عرض و ماره به اقطاب اربعه، متّحد می شوند و با معدل النّهار و منطقه البروج بر زوایای قائمه تقاطع می کنند و میل کلی همان میل اول و ثانی خواهد بود؛ و نیز اگر دو دائره موازی با یکدیگر باشند ابعاد همه اجزای آنها نسبت به یکدیگر به یک اندازه خواهند بود هرچند دو عظیمه متوازی بر کره متصوّر نمیشود؛ امّا دائره معدل النهار و منطقه البروج دو عظیمه متقاطع اند؛ و دائره میل و عرض بر هر جزوی از اجزای دیگر منطقه البروج بگذرند، دائره عرض با آن بر زوایای قائمه تقاطع می کند، و دائره میل به حاده و منفرجه که دو حاده متقابل برأس و دو منفرجه متقابل برأس خواهد بود، چنانکه دو دائره عرض و میل با یکدیگر.ب
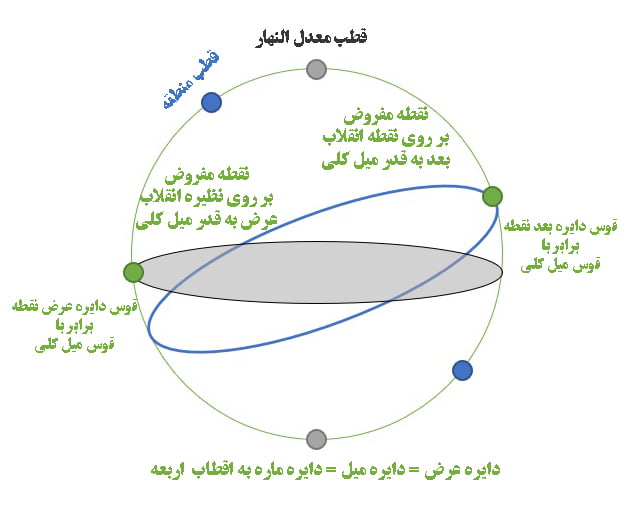
فرض کنیم –ا ح– معدل النّهار بر قطب –ه-.
و –ا ز– منطقه البروج بر قطب –و-.
و –ج– نقطه مفروض از اجزای منطقه البروج.
و –ز– رأس السرطان یعنی منقلب صیفی. و –ح– نظیره آن بر معدل.
پس –و ح– دائره ماره به اقطاب اربعه خواهد بود بر قطب –ا-، و –و د– عظیمه عرض، و –ه ب– دائره میل، و –ج ب– میل اوّل، و –ج د– میل ثانی، و –ر ح– میل کلی و میل اول و میل ثانی رأس السرطان.
در مثلث –ج ب د– زاویه –ج د ب– حاده است و –ج ب د– زاویه قائمه است و –ج د– وتر قائمه، أطول از –ب ج– وتر حاده است. چنانکه در شکل هفتم مقاله اولی اکرمانالاؤوس مبرهن شده است که: الزاویه العظمی من المثلث یوترها الضلع الأطول.
در هر مثلث اعم از مثلث در سطح مستوی و مثلث در سطح مستدیر که مثلث کروی است، ضلع مقابل هر زاویه را وتر آن زاویه گویند (به فتح واو و تاء) پس اضلاع سه گانه مثلث هر یک وتر زاویه مقابل خود است. و چنانکه در درس دوم گفته آمد در حقیقت وتر خط مستقیمی است که دائره را به دو پاره می کند؛ و چون زوایای مثلث هر یک زاویه مرکزی دائره ای هستند و درجات و دقائق هر قوس دائره مقدّر زوایای مرکزی آن دائره اند. پس در واقع ضلع مقابل هر زاویه مثلث وتر دائره ای است که آن زاویه مثلث، زاویه مرکزی آن دائره است. مانند مثلث –ا ب ج– وتر زاویه –ب– است یعنی وتر قوس –ا ج– مقدّر آن از دائره –ا ج د– است.
برای مطالعه درس سیزدهم دروس هیئت و دیگر رشته های ریاضی اینجا را کلیک کنید.
بیان (درس دوازدهم دروس هیئت – پیرامون میل (عرض و بعد کوکب))
الف)
بیان:
حالات مختلف بر اساس اشکال زیر
-
- اگر کوکب بر نفس معدل النهار بود آن را بعد نبود.
- اگر کوکب بر نفس معدل النهار بود آن را بعد نبود.
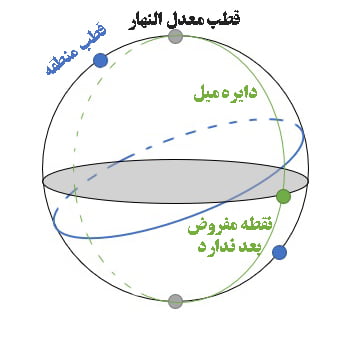
-
- اگر بر نفس منطقه البروج بود آن را عرض نبود. خورشید همیشه و در طول سال در سطح منطقه البروج بوده و هیچگاه عرض ندارد.
- اگر بر نفس منطقه البروج بود آن را عرض نبود. خورشید همیشه و در طول سال در سطح منطقه البروج بوده و هیچگاه عرض ندارد.
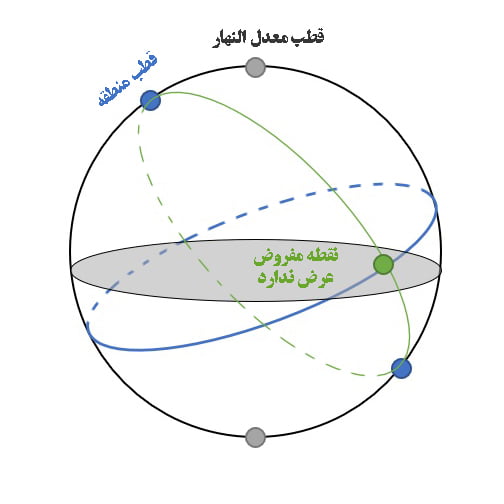
-
- اگر بر یکی از دو نقطه اعتدال بود او را نه بعد بود و نه عرض. در دو روز از سال خورشید نه تنها عرض ندارد بلکه میل نیز ندارد.
- اگر بر یکی از دو نقطه اعتدال بود او را نه بعد بود و نه عرض. در دو روز از سال خورشید نه تنها عرض ندارد بلکه میل نیز ندارد.
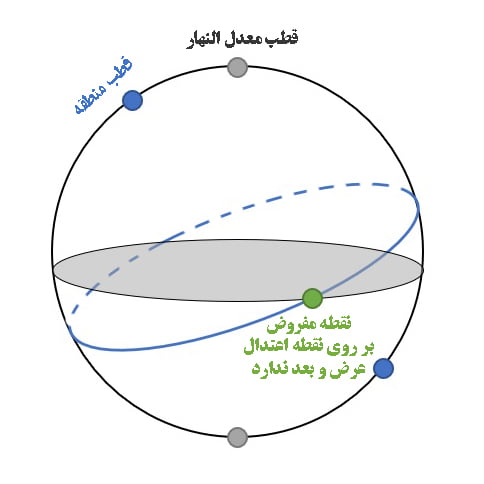
-
- اگر بر یکی از دو نقطه منقلب بود بعد او به قدر میل کلی بود. در دو روز از سال میل خورشید به قدر میل کلی است. این حداکثر میل خورشید در طول سال است.
- اگر بر یکی از دو نقطه منقلب بود بعد او به قدر میل کلی بود. در دو روز از سال میل خورشید به قدر میل کلی است. این حداکثر میل خورشید در طول سال است.
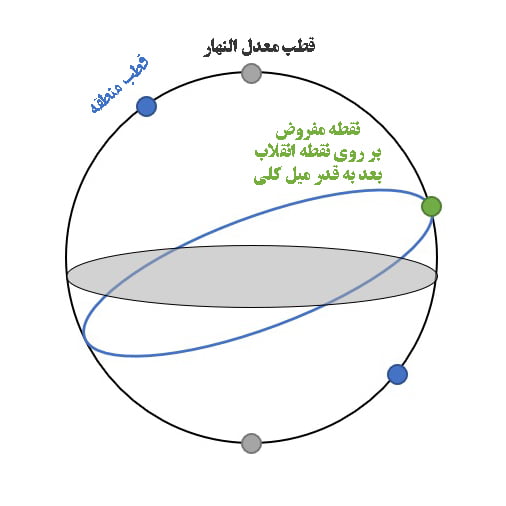
-
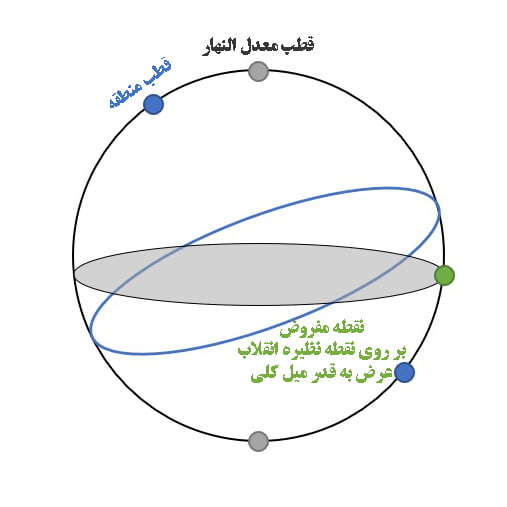
- اگر بر یکی از دو نقطه نظیره انقلاب بود عرض او به قدر میل کلی بود.
-
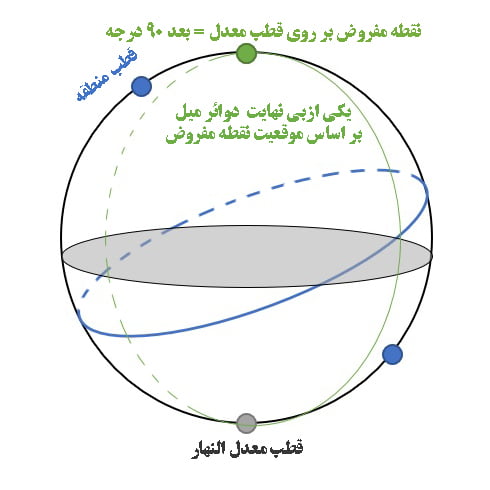
- اگر بر قطب معدل بود بعد او ربع دور بود.
-
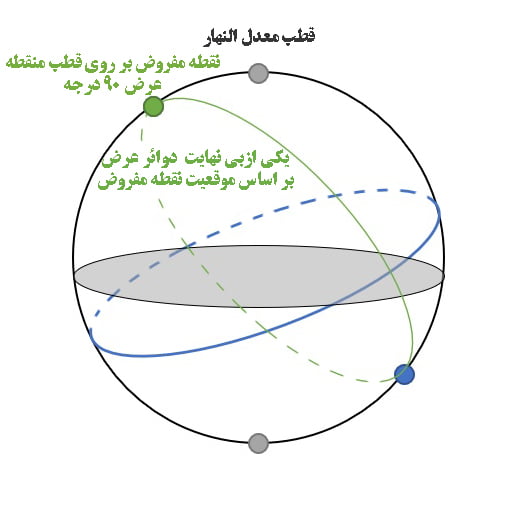
- اگر بر قطب منطقه بود عرض او ربع دور بود.
ب)
بیان:
به شرح شکل زیر
یادداشت
لازم به ذکر است که مطالب قیدشده فوق تحت عنوان بیان، نکات و … در حد فهم این نگارنده حقیر است، بنابراین اکیداً توصیه میگردد علاوه بر مطالعه اصل کتاب، پیگیری مستمر جلسات تدریس استاد صمدی آملی در خصوص شرح کتاب دروس هیئت و دیگر رشتههای ریاضی جناب علامه حسنزاده آملی، به مباحثه نیز بپردازید.
کتاب دروس هیئت و دیگر رشتههای ریاضی علامه حسنزاده آملی که توسط استاد صمدی آملی تدریس شده است.
مجله اینترنتی تحلیلک







