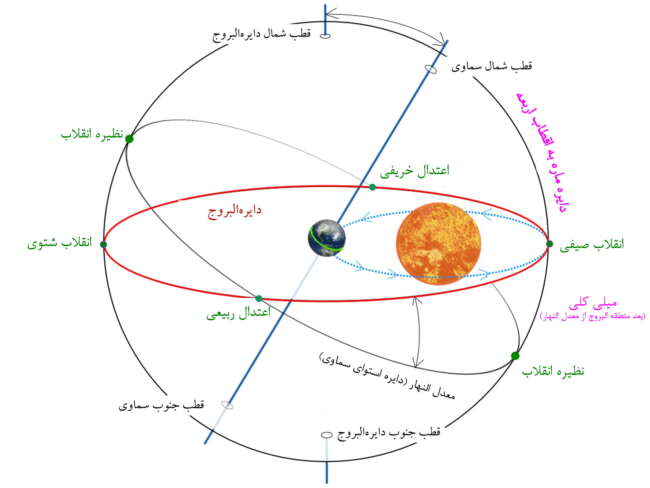
تعریف دایره ماره به اقطاب اربعه
این مطلب به درس هشتم کتاب دروس هیئت و دیگر رشته های ریاضی علامه حسن زاده آملی با عنوان دایره ماره به اقطاب اربعه اختصاص دارد.
درس 8
دایره ماره به اقطاب اربعه
هرگاه دائره ای بر قطب دائره ای گذرد مار بر قطب دیگرش نیز بود، و آن دائره هم با وی چنین بود یعنی هر یک بر دو قطب دیگری گذرد و تقاطع آن دو بر زوایای قائمه بود و بالعکس یعنی هرگاه تقاطع دو دائره با یکدیگر بر زوایای قائمه بود هر یک مارّ بر دو قطب دیگری بود که در درس قبل گفته آمد.الف
دایره ماره به اقطاب اربعه:
اگر عظیمه ای بر هر یک از دو قطب معدل النهار و منطقه البروج بگذرد یعنی مار بر چهار قطب این دو منطقه بود، آن را دایره ماره به اقطاب اربعه گویند. و سطح آن بر سطح هر دو منطقه بر زوایای قائمه قائم است. و دو قطب او دو نقطه اعتدال بود زیرا که این دائره بر قطبین هر دو آنها گذشته است پس لامحاله آن قطبین او محل تقاطع ایشان که مشترک بینهما است می باشد. پس قوسهایی از معدل النهار و منطقه البروج که بین هر یک از دو نقطه اعتدال و دائره ماره به اقطاب اربعه واقع شوند ربع دور خواهند بود.ب
و مدّت سیر شمس در دائره شمسیه در هر ربعی، فصلی از فصول اربعه سال در اکثر بقاع بود.
و دو نقطه تقاطع این دایره ماره به اقطاب اربعه با منطقه البروج را دو نقطه انقلاب گویند. آن نقطه انقلاب که در نیمه شمالی منطقه البروج بود انقلاب صیفی گویند که چون شمس بدانجا رسد اول تابستان در اکثر بقاع بود. و آن دیگر را که در نیمه جنوبی منطقه البروج بود انقلاب شتوی گویند که چون شمس بدانجا رسد اول زمستان در اکثر بقاع بود.ج
و دو نقطه تقاطع این دائره با معدل النهار را نظیره انقلاب گویند یکی را نظیره انقلاب صیفی و دیگری را نظیره انقلاب شتوی. این نظیره با جزء نظیر درس قبل اشتباه نشود.
بدان که چون خواهیم بر کره بعد نقطهای را از مبدئی مفروض و یا میل عظیمه ای را از دیگری تحصیل کنیم ناچار باید به وسیله ترسیم عظیمه ای بر آن بدست آوریم. خلاصه طناب مسّاحی ما باید قوس عظیمه ای بوده باشد.
و چون در تحصیل مسافت بعد، جانب اقرب لحاظ میشود، باید عظیمه ای که به منزلت طناب مساحی است از قطبین عظیمه مبدأ و نقطه مفروض بگذرد تا قوس بعد قائم بر عظیمه مبدأ گردد و اقصر قوس بین نقطه مفروض و مبدأ بود.
حال بدان که اقصر قوسی از دایره ماره به اقطاب اربعه در میان دو منطقه معدل النهار و منطقه البروج یا میان دو قطب ایشان افتد آن را میل کلّی گویند در ازای میول جزئیه ای که این دو منطقه را است.د
ا = نقطه اعتدال و قطب دائره ماره به اقطاب اربعه
ا ب = قوسی از معدل النهار که ربع دور است
ا ج = قوسی از منطقه البروج که ربع دور است
ج = نقطه انقلاب
ب = نظیره انقلاب
ح ب = میل کلی که قوسی از دائره ماره به اقطاب اربعه است
برای مطالعه درس نهم دروس هیئت و دیگر رشته های ریاضی اینجا را کلیک کنید.
بیان (درس هشتم دروس هیئت – دایره ماره به اقطاب اربعه)
الف)
بیان:
همانطور که در درس 7 و با در نظر گرفتن حالت های مختلف دو عظیمه در یک کره بیان شد، در صورتی که دایره ای از قطب دایره دیگر بگذرد، ناچار هم از قطب دیگر آن دایره خواهد گذشت و هم بر دایره دیگر عمود می شود و همینطور بلعکس (دایره دیگر نیز از قطب این دایره گذشته و عمود بر آن است – به عبارت دیگر هر دو دایره عمود بر یکدیگر و از قطب های یکدیگر عبور خواهند کرد)
ب)
بیان:
عظیمه ای را در نظر بگیرید که هم از دو قطب منطقه البروج و هم از دو قطب معدل النهار عبور کند. این عظیمه علاوه بر آن که مار بر چهار قطب یاد شده است بر هر دو دایره نیز عمود خواهد بود. از سوی دیگر بر اساس مطالب بند قبل، هر گاه دایره ای از قطبین دایره دیگر عبور کند، آن دایره نیز از قطبین دایره اول عبور خواهد کرد (همانند حالت عمود دو دایره که در بیان درس هفت بدان اشاره شد).
حال با توجه به وضعیت دایره ماره به اقطاب اربعه نسبت به هر یک از دایره های منطقه البروج و معدل النهار، هر یک از آنها نیز می بایست از قطبین دایره ماره به اقطاب اربعه عبور کند و از آنجا که دایره ماره به اقطاب اربعه مذکور دارای دو قطب ثابت است، پس برای گذشتن دو دایره معدل النهار و منطقه البروج از قطبین یاد شده، نقطات مذکور (قطبین دایره ماره) نقطه طلاقی و برخورد دو دایره منطقه البروج و معدل النهار خواهد بود که این دو نقطه بر اساس مطالب اشاره شده در درس قبل، نقاط اعتدال هستند.
بر این اساس دایره منطقه البروج و معدل النهار بر اساس دو نقطه اعتدال (محل طلاقی دو دایره و محل قطبین دایره ماره به اقطاب اربعه) و بر اساس محل عبور دایره ماره به چهار ربع مساوی تقسیم خواهند شد.
ج)
بیان:
دو نقطه تقاطع دایره ماره به اقطاب اربعه با منطقه البروج را انقلاب صیفی و شتوی می نامند که بر اساس آنها و دو نقطه اعتدال ربیعی و خریفی (مطالب درس هفتم) منطقه البروج به چهار ربع برابر که مدت سیر خورشید نیز در هر یک از آنها یک چهارم سال خواهد بود، چهار فصل سال شمسی را تشکیل خواهند داد. به عبارت دیگر حرکت خورشید به روی منطقه البروج بر اساس 365 روز سال و قرار گرفتن آن در هر یک از این چهار ربع، فصل های مختلف را پدید می آورد.
د)
بیان:
دایره میل (به صورت جمع میول) زمانی رسم می گردد که بخواهیم فاصله یا بعد کوکب، ستاره، عظیمه و … را از معدل النهار محاسبه کنیم. به عبارت دیگر میل کلی در واقع بعد و فاصله منطقه البروج از معدل النهار است.
به همین ترتیب میول جزئیه منطقه از معدل النهار، میل (فاصله) نقاط دیگری جز نقاط انقلاب منطقه البروج است از معدل النهار که برای محاسبه آن تنها به دایره ای نیاز است که از دو قطب معدل النهار و نقطه مفروض منطقه البروج گذشته باشد که در این صورت عمود بر معدل بوده و قوس میان معدل و نقطه مفروض منطقه البروج میل جزئی آن نقطه است.
یادداشت
لازم به ذکر است که مطالب قیدشده فوق تحت عنوان بیان، نکات و … در حد فهم این نگارنده حقیر است، بنابراین اکیداً توصیه میگردد علاوه بر مطالعه اصل کتاب، پیگیری مستمر جلسات تدریس استاد صمدی آملی در خصوص شرح کتاب دروس هیئت و دیگر رشتههای ریاضی جناب علامه حسنزاده آملی، به مباحثه نیز بپردازید.
کتاب دروس هیئت و دیگر رشتههای ریاضی علامه حسنزاده آملی که توسط استاد صمدی آملی تدریس شده است.
مجله اینترنتی تحلیلک