تعریف مدارات عرضی در دروس هیئت

این مطلب به درس ششم کتاب دروس هیئت و دیگر رشته های ریاضی علامه حسن زاده آملی با عنوان تعریف تعریف مدارات عرضی اختصاص دارد.

درس ۶

منطقه البروج و مدارات عرضی

هرگاه دو دائره عظیمه کره ای در یک سطح نباشند یکدیگر را در دو نقطه به تناصف تقاطع کنند. یعنی هر یک از این دو منطقه بر آن دو نقطه به دو نیمه شود، و از هر نقطه تقاطع چهار زاویه پدید آید. پس اگر در این صورت سطح یک دائره بر سطح دائره دیگر قائمه باشد هر یک از آن زوایا قائمه بود که قوس مقدّر آن ربع دور یعنی نود درجه بود؛ و اگر قائمه نباشد تقاطع ایشان بر زوایای حاده و منفرجه باشد. قوس مقدر زاویه حاده کمتر از ربع، و منفرجه بیشتر از آن بود.

حال بدان که دایره منطقه البروج از سطح معدل النهار مایل است که نه در سطح دایره معدل النهار است، و نه قائم بر آن لاجرم با وی به تناصف بر زوایای حاده و منفرجه تقاطع کند. و محور این حرکت با محور معدل النهار بر مرکز عالم متقاطع شود هم بر زوایای حاده و منفرجه.^الف

چون تقاطع یاد شده به تناصف است پس آن دو نقطه تقاطع، دو نقطه متقابل و متقاطر خواهند بود؛ و هر نیمه محیط عظیمه نصف دور یعنی ۱۸۰ درجه. و از فلک بروج یک نیمه در جانب شمال معدل النهار باشد، و یک نیمه در جانب جنوب آن.^ب

و چون منطقه البروج دایره شمسیه است که مدار شمس در سطح آنست، ناچار مدار شمس با دایره معدل النهار در همان دو نقطه تقاطع کند، و نسبت او با معدل چنان است که دایره منطقه البروج با وی.^ج

هر نقطه ای که در دو طرف منطقه البروج بر کره فرض کنند، مدار آن که بسبب حرکت ثانیه رسم می شود دایره صغیره ای متوازی با دایره منطقه البروج بود؛ و این مدارات را مدارات عرضی گویند به بیانی که گفته آید. وزان مدارات عرضی به منطقه البروج، وزان مدارات میول یعنی مدارات یومی به معدل النهار است.^د

حرکت فلکی اگر از مغرب به مشرق بوده باشد آن را حرکت به توالی ‌گویند، و عکس آن را که حرکت از مشرق به مغرب است حرکت به خلاف توالی گویند چنان که در درس بعد دانسته خواهد شد. و این اصطلاح که حرکت به توالی و خلافت توالی است در این فن بسیار رائج است.

برای مطالعه درس هفتم دروس هیئت و دیگر رشته های ریاضی اینجا را کلیک کنید.

(درس ششم دروس هیئت – تعریف مدارات عرضی)

بیان

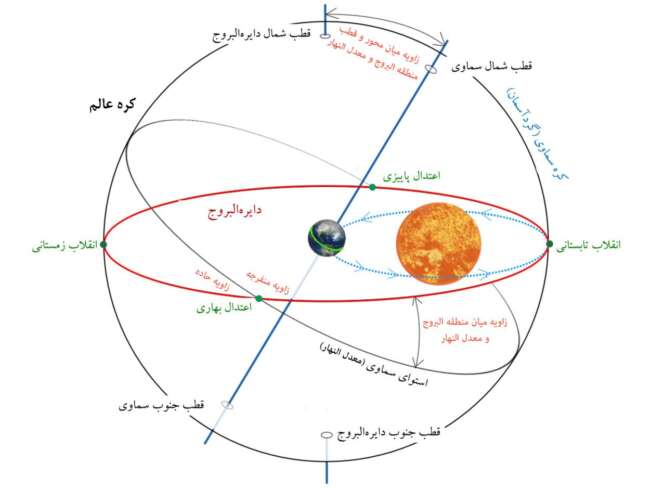
الف)
بیان:
بر اساس شکل فوق، کره عالم با مرکزیت زمین در نظر گرفته شود. دایره منطقه البروج و معدل النهار و همچنین زاویه میان آنها و میان قطبین و محور آنها نیز در شکل مشخص است.

ب)
بیان:
دو نقطه اعتدال بهاری و اعتدال پاییزی (که در درس های آتی با آنها آشنا خواهیم شد) دو نقطه تقاطع دایره معدل النهار و دایره منطقه البروج بوده که دو نقطه متقابل و متقاطر هستند و فاصله میان آنها از هر سمت (بر روی محیط دایره ها) ۱۸۰ درجه است.

همانند کره عالم که بر اساس معدل النهار به دو نیمه شمالی و جنوبی تقسیم می شود، منطقه البروج نیز دارای نیمه شمالی و جنوبی است.

ج)
بیان:
هرچند در شکل به ظاهر اندازه دایره شمسیه کوچکتر نمایش داده شده است (برای نمایش جزئیات بیشتر) اما همانطور که مشخص است مسیر حرکت خورشید با منطقه البروج یکسان بوده و دایره های ترسیم شده در یک سطح اند. بنابراین خورشید نیز در دو نقطه از سال (نقاط اعتدال) بر روی معدل النهار قرار میگیرد (دایره حرکت آنها متقاطع می شود)

د)
بیان:
در حرکت ثانیه (حرکت بر اساس منطقه البروج) نیز همانند حرکت اولی (حرکت بر اساس معدل النهار) دارای دایره های کوچکتر موازی با منطقه بر اساس نقاط مفروض هستند که البته به دایره های موازی منطقه البروج، دایره های عرضی گرفته می شود.

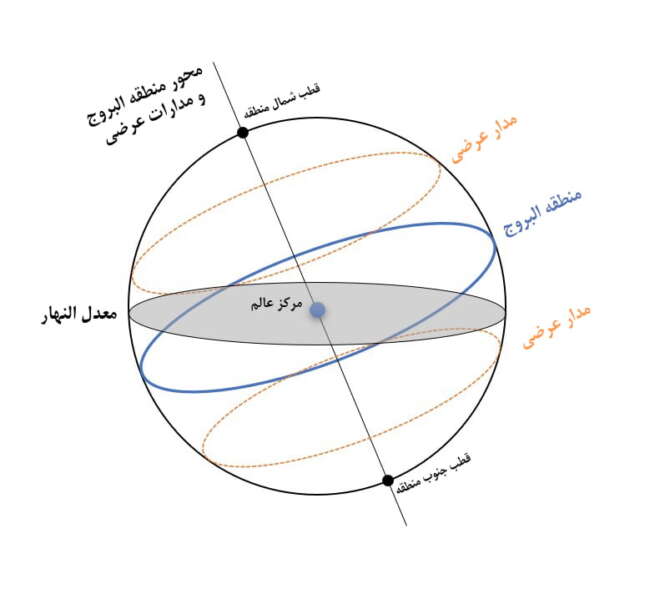
یادداشت
لازم به ذکر است که مطالب قید شده فوق تحت عنوان بیان، نکات و … در حد فهم این نگارنده حقیر است، بنابراین اکیداً توصیه می‌گردد علاوه بر مطالعه اصل کتاب، پیگیری مستمر جلسات تدریس استاد صمدی آملی در خصوص شرح کتاب دروس هیئت و دیگر رشته‌های ریاضی جناب علامه حسن‌زاده آملی، به مباحثه نیز بپردازید.

کتاب دروس هیئت و دیگر رشته‌های ریاضی علامه حسن‌زاده آملی که توسط استاد صمدی آملی تدریس شده است.

مجله اینترنتی تحلیلک