این مطلب به درس اول کتاب دروس هیئت و دیگر رشته های ریاضی علامه حسن زاده آملی با عنوان قطر، دایره عظیمه و صغیره اختصاص دارد.
درس 1
قطر، دایره عظیمه و صغیره
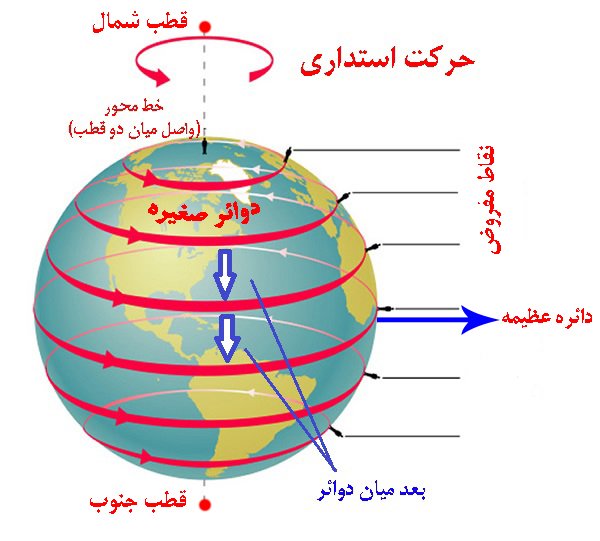
چون کره بر نفس خود حرکت کند و یا فرض حرکت آن شود، هر نقطه ای که بر محیط آن فرض شود بدین حرکت استداری که اوضاع آن نسبت به جز او مبدل میگردد، بعد از تمامی دوره، دایره ای تامه رسم کند، مگر دو نقطه متقابل که دو قطب کره و دو قطب حرکت اند.الف
و خطی مستقیم که واصل میان دو قطب است قطری است که آن را محور گویند و آن نیز ساکن است که کره بر آن می گردد و قطر آن خط مستقیم است که به مرکز دایره یا کره بگذرد.ب
و هر دو نقطه متقابل دو طرف قطری از اقطار کره را دو نقطه متقاطر گویند پس دو قطب حرکت و یا دو قطب کره دو نقطه متقاطر خواهند بود.
و آن دوائر مرتسمه از نقاط مفروضه را مدارات آن نقاط گویند و از آنها به نحو اطلاق تعبیر به مدارات می کنند و دو قطب کره را دو قطب هر یک از این مدارات میگویند.ج
و این دوائر یا با یکدیگر متحد باشند و یا متوازی. و دو خط متوازی خواه مستدیر و خواه مستقیم آن باشند که بعد میان آن دو به یک اندازه باشد. یعنی هر نقطه ای که بر یکی از آن دو فرض کنند بعد همه از آن خط دیگر برابر باشد.د
از این دوائر فقط یک دایره عظیمه است که بر مرکز کره میگذرد و بعد او از قطبین مساوی است و آن را منطقه کره گویند، بدین نظر که منطقه کمربند است و آن دائره بر میان کره گذرد. و دوائر دیگر را صغیره گویند.ه
برای مطالعه درس دوم دروس هیئت و دیگر رشته های ریاضی اینجا را کلیک کنید.
درس اول: قطر، دایره عظیمه و صغیره
بیان
الف)
بیان: بر اساس شکل رسم شده، در حرکت استداری کره کلیه نقاط مفروض بر سطح آن پس از یک دوره حرکت کامل، دایرهای ترسیم میکنند که البته این موضوع در خصوص دو نقطه قطب حرکت که به دلیل قرار داشتن بر روی محور حرکت، عملاً بدون حرکت باقی میمانند، صدق نمیکند. لفظ ظاهراً برای حرکت دو قطب از آنجهت است که این دو نقطه به دور خود میچرخند.
یادآوری: حرکت استداری یا حرکت دورهای، به حرکتی گفته می شود که از یک نقطه شروع و پس از گردش یک مسیر دایرهای به نقطه اولیه خود باز میگردد. بهعبارتدیگر از مسیر حرکت یک دایره را ترسیم میکند.
معنی “تامه“: کامل
نکته: از منظر علمی، دایره بهصورت دوبعدی بوده و یک سطح است و نه یک خط
ب)
بیان: دلیل نامگذاری قطر واصل میان دو قطب به نام محور از آنجهت است که کره مذکور حول این خط به دور خود میچرخد.
ج)
بیان: محور حرکت و همچنین دو قطب حرکت برای تمامی مدارات ایجادشده در حرکت استداری کره مشترک است.
د)
بیان: از آنجا که حرکت حول یک محور صورت میگیرد، نقاط مفروض که دایرههای مختلف ترسیم میکنند، ممکن است دایرههای متحد ترسیم کنند (درصورتی که بر روی یک دایره قرار داشته باشند) و در غیر این صورت حتماً دایرههای ترسیمشده به صورت موازی هستند.
“مستدیر“: دایرهای – “بعد“: فاصله
ه)
بیان: مدارات و یا همان دایرههای رسم شده از حرکت استداری نقاط بر سطح کره، از مرکز کره (از آنجا که دایره سطح است و کره حجم، کره در میانه خود دارای مرکز است که یک دایره از آن عبور میکند) شروع تا دو قطب ادامه مییابند و به همین ترتیب از مرکز به سمت قطبین اندازه آنها کوچکتر می شود، بهطوری که دایره مرکزی (دایره عظیمه) بزرگترین بوده و نزدیکترین دایره به قطب (یکی از دایره های ضغیره) کوچکترین است که بزرگترین دایره، منطقه یا کمربند نام دارد.
نکات کلی
بهطورکلی 11 دایره عظیمه مورد بحث قرار خواهد گرفت. هرچند که 2 دایره عظیمه قابل ادغام است که در درس های آتی با آنها آشنا خواهیم شد.
محاسبات علم هیئت تنها از طریق دایره های عظیمه امکانپذیر خواهد بود و دایرههای صغیره جایگاهی در محاسبات نداشته و صرفاً در برخی مباحث تئوری مورد بررسی قرار میگیرد.
یادداشت
لازم به ذکر است که مطالب قیدشده فوق تحت عنوان بیان، نکات و … در حد فهم این نگارنده حقیر است، بنابراین اکیداً توصیه میگردد علاوه بر مطالعه اصل کتاب، پیگیری مستمر جلسات تدریس استاد صمدی آملی در خصوص شرح کتاب دروس هیئت و دیگر رشتههای ریاضی جناب علامه حسنزاده آملی، به مباحثه نیز بپردازید.
کتاب دروس هیئت و دیگر رشتههای ریاضی علامه حسن زاده آملی که توسط استاد صمدی آملی تدریس شده است.
مجله اینترنتی تحلیلک








