این مطلب به بخش چهارم از رساله میل کلی علامه حسن زاده آملی که در مرداد و شهریور سال 1362 در ماهنامه مجله دانشگاه انقلاب به چاپ رسیده است، با عنوان تحصیل مقدار میل کلی اختصاص دارد.
سبب تقدیم معرفت میل کلی
در زیجات ابتدا بحث میل کلی و طرق تحصیل آنرا ذکر کرده اند، سبب تقدیم آنرا علامه نیشابوری در شرح فصل یازدهم مقاله اولی مجسطی عنوان کرده است، وی گوید: سبب تقدیم معرفت میل کلی این است که تا میل کلی معلوم نگردد راهی به معرفت مطالع فلک مستقیم نیست، و هرگاه مطالع فلک مستقیم معلوم نگردد به معرفت مطالع آفاق مائله و سائر آنچه که متعلق بدانست راهی نیست، و نیز میول جرئیه شمس تا میل کلی معلوم نباشد تحصیل نتوان کرد. الخ (نقل به ترجمه)
تحصیل مقدار میل کلی
در تحصیل مقدار میل کلی طرق گوناگون در کتب فن آورده اند. بطلیموس در فصل یازدهم مقاله اولی مجسطی، و خواجه در تحریر آن دستور ساختن دو آلت نجومی برای معرفت مقدار میل کلی و عروض بلاد داده اند. میل کلی و میول جزئیه را با اسطرلاب و ربع مجیب و با بسیاری از آلات نجومی دیگر نیز میتوان تحصیل کرد:
آفاق بر سه قسم تقسیم میگردد قسمی ذوظلین است، و قسمی ذوظل واحد است، و قسمی ذوظل دائر. این ظل، ظل شاخص قائم بر سطح افق است.
هنگامی که شمس در یکی از دو نقطه انقلاب به دائره نصف النهار رسیده است دائره ماره به اقطاب اربعه و دائره نصف النهار و دائره ارتفاع یکی خواهند شد و قوسی از آنها که بین مدار یکی از دو انقلاب و معدل النهار از جانب اقرب واقع شود، قوس میل کلی است. و قوسی که میان دو قطب معدل و دائره بروج از جانب اقرب واقع میشود معادل میل کلی است. و قوسی که واقع بین مدار هر یک از دو انقلاب و دائره افق واقع است غایت ارتفاع آن منقلب است.
بنابراین، در آفاق قسم اول (ذوظلین) اصغر ارتفاع جنوبی شمس با اصغر ارتفاع شمالی آن جمع، و فضل نصف دوور بر این مجموع اخذ گردد، این فضل ضعف میل کلی است که نصف آن مقدار میل کلی است.
مثلاً در این سال اصغر ارتفاع جنوبی مکه مکرمه را گرفتیم شد: 45 درجه و 9 دقیقه و 10 ثانیه و اصغر ارتفاع شمالی آنرا گرفتیم شد: 87 درجه و 59 دقیقه و 20 ثانیه
جمع آن دو شد:
![]()
فضل نصف دور بر این مجموع شد:
![]()
نصف این فضل مساوی با میل کلی است:
![]()
تحصیل مقدار میل کلی
و در آفاق قسم دوم فضل اعظم ارتفاعات شمس بر اصغر آن گرفته میشود، نصف این فضل قوس میل کلی است.
و در آفاق قسم سوم یا ظل ول مقیاس اعنی شاخص در یک روز فقط دور میزند (یعنی آفاقی که عرض آنها بقدر تمام میل کلی است) و یا اکثر از یک روز دور میزند و اقل از نصف سنه است (مواضعی که عرض آنها ازید از تمام میل کلی است و به ربع نرسیده است) و یا بقدر نصف سنه است (عرض تسعین) در این صورت اخیر اعظم ارتفاعات قوس میل کلی است چه معدل النهار و افق یکی است. و در صورت نخستین که ظل فقط یک روز حول مقیاس دور میزند (و آن روزی است که شمس در راس الجدی یعنی منقلب شتوی است) نیز اعظم ارتفاعات شمس اخذ و تنصیف میگردد این نصف، قوس میل کلی است. و در صورت دوم که ظل، حول مقیاس بیش از یک روز و کمتر از نصف سنه، دور میزند دو غایت ارتفاع جهت شمال و جنوب اخذ میشود که نصف این مجموع قوس میل کلی است.
غیر از طریق ارتفاع منقلبین در تحصیل میل کلی، طرق دیگری نیز موجود است از آن جمله طریقی است که علامه بیرونی در باب اول مقاله چهارم قانون مسعودی که مجسطی اسلامی است عنوان کرده است. (ص 366 ج 1)
تحصیل مقدار میل کلی
برهان هندسی بر اینکه میل کلی، اعظم میول است
ابتدای میل منطقه از معدل، نقطه اعتدال است، و سپس تا نقطه انقلاب رو به تزاید میرود و آنجا غایت میل است. و چنانکه در قبل گفته ایم این قوس میل کلی، قوسی از دائره ماره به اقطاب اربعه است. در اصطلاح فن هیئت نقطه تقاطع ماره باقطاب اربعه و منطقه البروج را نقطه انقلاب، و نقطه تقاطع آنرا با معدل نظیره انقلاب گویند. یکی نظیره انقلاب صیفی و دیگر نظیره انقلاب شتوی.
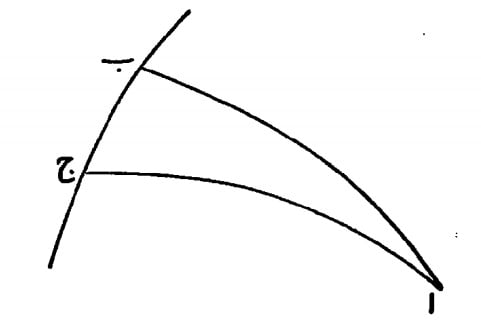
در مثلث ا ب ج، ا نقطه اعتدال است و ا ج نقطه بروج و ج نقطه انقلاب و ب نظیره آن و ب ج قوسی از ماره باقطاب اربعه که میل اعظم است و هر یک از 1 ب، ا ج، ربع دور است.
و هر یک از دو زاویه ا ب ج، ا ج ب زاویه قائمه است. چه در مثلث کروی زوایای سه گانه مثلث مستوی از 180 درجه (و قائمه) است، آن مثلث مستوی است که مجموع زوایای ثلاث آن معادل دو قائمه است.
در شکل سی و دوم مقاله اولی اصول اقلیدس مبرهن شده است که مثلث مستوی زوایای ثلاث آن مساوری دو قائمه است، و در شکل یازدهم مقاله اولی اکرمانالاووس مبرهن شده است که مثلث کروی جمیع زوایای ثلاث آن اعظم از دو قائمه است.
تحصیل مقدار میل کلی
و هریک از ا ب، ا ج وتر زاویه قائمه و ربع دور است و جیبی (سینوس) اعظم از جیب قائمه یعنی جیب ربع نیست بنابراین دو مثلث مذکور بشکل مغنی:

پس جیب میل اعظم (جیب قوس ب ج که وتر زاویه حاده ب ا ج است) اعظم از باقی جیوب قوسهای میول دیگر است و همچنین قوس آن که ب ج است.
تحصیل مقدار میل کلی
تزاید میل کلی بر سبیل تناقص است
این بحث را خواجه نصیرالدین طوسی در تحریر اکرمانالاووس، و قاضی زاده رومی در شرح ملخص هیئت چغمینی عنان کرده اند. سخن در این است که از نقطه اعتدال تا انقلاب ربع دور است و میل منطقه البروج از معدل هرچند که از نقطه اعتدال تا بغایت میل اعظم رو به تزاید میرود ولی تزاید میل ربع دور چنین نیست که مثلاً به نسبت تزاید اجزای ربع تزاید بیابد، لذا از نقطه اعتدال تا نقطه انقلاب با اینکه ربع دور است، میل که از صفر تا بغایت رسیده است مقدار غایت از نصف ربع کمتر است (که 23 درجه و 25 دقیقه و 50 ثانیه است)
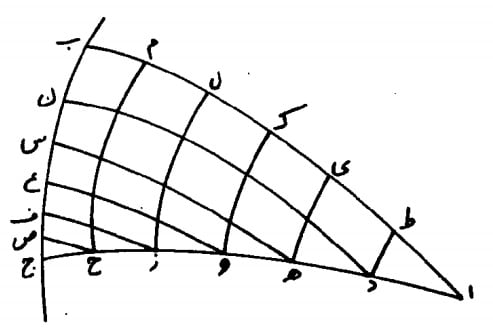
در بیان آن گوییم از نقطه اعتدال تا انقلاب را مثلاً به شش قسم متساوی تقسیم می کنیم که هر قسمی 15 درجه میشود و آن قوسهای ا د-تا-ح ج است، سپس از نقاط پنچگانه د ه و ز ح قوسهای صغار موازی دائره ماره باقطاب اربعه ترسیم می کنیم که قطب همه آ اعنی منقطه اعتدال است و عمود بر معدل النهارند که با آن برابر زوایای قائمه تقاطع می کنند.
قوس د ط میل قوس ا د است که معادل ن ب است، زیرا د ن-تا-ح ص از مدارات یومیه اند که دوائر صغار موازی معدل النهارند، و قوسهای موازی دائره ماره به اقطاب اربعه که د ط-تا-خ م اند، آنچه که در میان هر دو مدارات یومیه یا معدل النهار و هر یک از آن مدارات یومیه قرار گرفته است به حسب درجه با هم برابرند. یعنی د ط مثلاً مساوی با ن ب است و ه ی با س ب و هکذا.
حال گوییم که قوس میان ب ن بزرگتر از ن س است و ن س بزرگتر از س ع و هکذا.
پس نتیجه این شد که میل ا ه که ه ی است اعنی س ب است، بزرگتر از میل ا د که د ط اعنی ن ب است میباشد و میل زیاد شده است یعنی س ن بر ن ب افزوده شده ولی علی سبیل تناقص که میل 15 درجه دوم کمتر از میل 15 درجه اول است هرچند میل دوم بر اول افزوده میشود و میل به تزاید میرود.
برهان هندسی این مطلب شکل پنجم و ششم مقاله سوم اکرثاوذوسیوس است: اذا فصلت من عظیمه قائله عن عظیمه اخری (کدائره البروج المائله عن المعدل االعکس) قسی متساویه متتالیه مبتدئه من تقاطعهما (کالاعتدال) منتهیه الی غایه البعد بینهما (کالانقلاب و نظیرته) و رسمت دوائر موازیه للعظیمه الاخری ماره بالنقط الحادثه (کالمدارات الیومیه الموازیه لمعدل النهار، اوالمدارات العرضیه الموازیه لمنطقه البروج) فان تلک الدوائر تفصل من الدائره الماره باقطاب العظیمتین (کالماره بالاقطاب الاربعه) قسیاً متلفه فماقرب منها (ای من تلک القسی المختلفه من الماره بالاقطاب الربعه) الی العظیمه الاخری اعظم مما بعد عنها (ای عن العظیمه الاخری)
خواجه طوسی در تحریر اکرمانالاووس در ذیل شکل بیست و یکم مقاله دوم آن بیانی ارزشمند در پیرامون برهان مذکور اعنی شکل پنجم و ششم مقاله سوم اکرثاوذوسیوس دارد آنجا که می فرماید: اقول و هذا بیان ما ذکر فی الشکل الخامس و السادس من المقاله السادسه من اکرثاوذوسیوس فانه بین فی الخامس اخیر هذین الحکمین و منه یعلم فی الهیئه ان حصه کل قوس تقرب من نقطه الانقلاب من المیل تکون اصغر من حصه کل قوس تساویها و تکون ابعد منها من المیل. الخ
تحصیل مقدار میل کلی
میل قوسهای متساوی البعد از نقطه اعتدال متساوی است
بدانکه میل قوسهای متساوی البعد از نقطه اعتدال متساوی است و برهان آن در شکل بیست و دوم مقاله دوم اکرمانالاووس است: اذا تقاطعت دائرتان عظبمتان علی کره و فصلت من احدیهما قوسان متساویتان متسایتها البعد عن نقطه المتقاطع و اخرجت دوائر عظام من قطب احدی الدائرتین الی اطرافهما فانها تفصل من الدائره الاخری قوسین متساویتین الخ.
برای مطالعه بخش پایانی رساله میل کلی علامه حسن زاده آملی اینجا را کلیک کنید.
مجله اینترنتی تحلیلک









